Обратная функция — функция y=g(x), которая получается из данной функции y=f(x), если из отношения x=f(y) выразить y через x.
Чтобы для данной функции y=f(x) найти обратную, надо:
1.В соотношении y=f(x) заменить x на y, а y — на x: x=f(y) .
2.В полученном выражении x=f(y) выразить y через x.
Функции f(x) и g(x) — взаимно обратны.
Примеры нахождения обратных функций:
1) y=3x-8
1. x=3y-8
2. 3y=x+8
y=(x+8)/3.
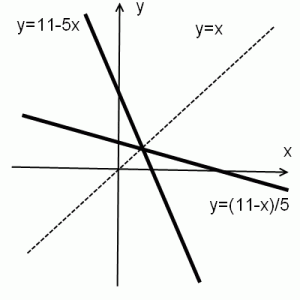
2) y=11-5x
1. x=11-5y
2. 5y=11-x
y=(11-x)/5.
Область определения и область значений функций f и g меняются местами: область определения f является областью значений g, а область значений f — областью определения g.
Не для всякой функции можно указать обратную. Условие обратимости функции — ее монотонность, то есть функция должна только возрастать или только убывать. Если функция не монотонна на всей области определения, но монотонная на некотором промежутке, тогда можно задать обратную ей функцию только на этом промежутке.
Пример обратных функций, заданных на промежутке.
y=x².
Это — квадратичная функция. Она убывает на промежутке (-∞;0), и
возрастает на промежутке (0;∞). Возьмем промежуток [0;∞). На этом промежутке функция монотонна, поэтому обратима. Ищем обратную функцию.
1. x=y²
2. y=√x.
y=x² и y=√x на [0;∞) — взаимно обратные функции.
Графики взаимно-обратных функций симметричны относительно прямой y=x.